Analyzing and Improving Our Learning Models

Now that we have some learning models under our belt, how do we improve upon a specific one? There are many options you can do like getting more training examples, increasing number of features, adding polynomial features, decreasing the learning rate, or changing the regularization term. Out of these options is there a way to decide which one would work the best for your specific algorithm? I say yes!

So usually people split up the data set into a training set and a testing set. This would eliminate the problem of overfitting, as you train the model on the first set, and then find the test error on the other set. The split percentage is usually 65/35 respectively. For linear regression, the test error stays the same as before

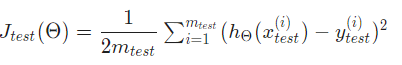
For classification tasks, the error will be

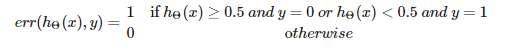
Basically like a logistic regression/neural network which says if the hypothesis returns true (h(x) >= 0.5) and y is 0 (false), there would be a 1 outputted signifying error. So, from this formula we can add together all the errors over the testing set and then divide that value by the number of elements in the testing sets to the get what percent did we get wrong. For example, if there were four testing examples and two of those our neural network got wrong, the classification error would be 50 percent because the two wrong (1 + 1) divided by the total number of elements(4) is 2/4 = 50%. The mathematical formula is written out below:

We need to make sure that we do not choose the learning model that overfits the test data, hence, we introduce a cross validation test. So after training on the training set, we put our code through the cross validation test and choose the polynomial formula/features that make the learning model have the lowest error rate, and then use the update learning model on the test set to get our test error.

Let us now talk about bias and variance. Basically, a high bias mean the learning model is underfitting the data and a high variance means that the data is prone to overfitting the training test. To fully understand these two terms let us look at the following diagram.

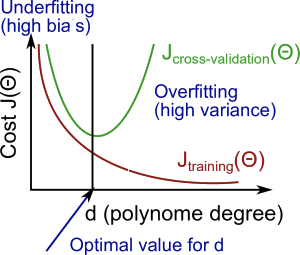
The optimal polynomial degree to have for the learning model is where the cross validation is minimized. The reason is because if we make the learning model not very complex, it will underfit our data, creating high bias. You can see on the left of the graph that when a learning model underfits, the training cost is very high, and so is the cross validation error. They are both similar numbers. However, if you make the polynomial very complex it will overfit, creating high variance. On the graph you can see that the training cost is very low with complex polynomials, but the cross validation test set is high.  

There will be a more detailed explanation of bias/variance in the next post!