Vectorizing Nueral Networks

We can also do a vectorized implementation of the activation functions for the nodes.

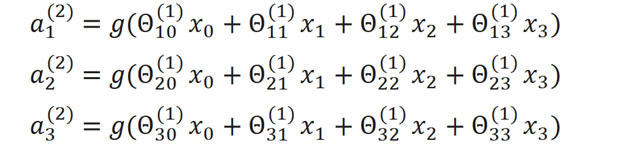
We can use a new variable called z (subscript k exponential j) that represents what is inside of g function. So for the second layer’s activation we can represent it as:

So layer 2 (j=2) and node k, the variable z will be

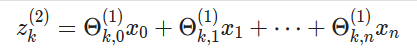
So if we create two vectors, one of the x values (in the first layer) and one of the z values, z will be one element shorter than x because of the bias so it would look like:

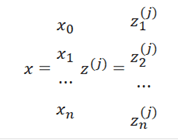
Instead of saying x is the base value, just set x to be the “activation” of the corresponding node in the base layer. So x = a(1 superscript)

Now we can generally make the statement that:

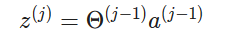
Above, we are multiplying the matrix theta which has dimensions of

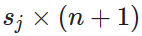
(where sj is the total number of activation nodes in the next layer and n represents the total input layers) with the vector a which has height of n + 1 (it is n+1 because it is accounting for the bias unit). The resulting vector will have height of sj, successfully giving us the next layer of activation nodes. Hence, we can generalize the above theorem to just:

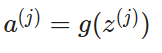
After we compute this value, we can just add the bias node and calculate the z value for the next layer of nodes (remember our graph looks like)

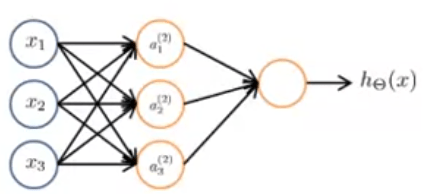
This will give us out final node! So if we follow the same steps we get that the next vector z will be equal to theta(2) * a(2). Our final theta matrix will only have one row, so sj = 1, and there will only be one column of activation nodes as usual. Therefore, we will get a single number by multiplying this row by a column. More formally:

And since z(j+1) is simply a number this function, the very last step of our neural network, is basically just acting like linear regression. Hence, neural networks are really just a coagulation of many, many, many steps of linear regression giving a complex and accurate answer.